CINEMATICA: ACELERACION

Aceleración

Analogamente vamos ahora a definir la función vectorial de la aceleracion:

$\overrightarrow a (t) = \lim _{\Delta t \to 0} \frac{{\Delta \overrightarrow v }} {{\Delta t}} = \frac{{\operatorname{d} \overrightarrow v }} {{\operatorname{d} t}} = \dot\vec v = \ddot\vec r \,.$

La función vectorial de la aceleracion provienen de las componentes escalares de la función velocidad y de la función posición, así:

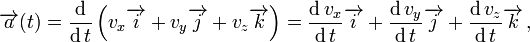
$\overrightarrow a (t) = \frac{\operatorname{d} } {{\operatorname{d} t}}\left( {v_x \overrightarrow i + v_y \overrightarrow j + v_z \overrightarrow k } \right) = \frac{{\operatorname{d} v_x }} {{\operatorname{d} t}}\overrightarrow i + \frac{{\operatorname{d} v_y }} {{\operatorname{d} t}}\overrightarrow j + \frac{{\operatorname{d} v_z }} {{\operatorname{d} t}}\overrightarrow k \,,$

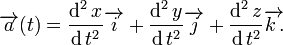
$\overrightarrow a (t) = \frac{{\operatorname{d} ^2 x}} {{\operatorname{d} t^2 }}\overrightarrow i + \frac{{\operatorname{d} ^2 y}} {{\operatorname{d} t^2 }}\overrightarrow j + \frac{{\operatorname{d} ^2 z}} {{\operatorname{d} t^2 }}\overrightarrow {k\,.}$

Como se conoce, son las componentes escalares del vector velocidad igual a la direccion de la velocidad instantantea en los ejes de coordenadas.

En sentido contrario se puede hallar por integracion las correspondientes funciones.

Ejemplo: Para la caida libre con velocidad inicial v₀ de un punto con el vector posición r₀ (vertical o lanzamiento curvo).

Cuando el eje Z (vector unitario k) esta dirigido verticalmente hacia abajo, es

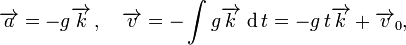
$\overrightarrow a = - g\overrightarrow k \,,\quad \overrightarrow v = - \int {g\overrightarrow k \,\operatorname{d} t = - g\,t} \overrightarrow k + \overrightarrow v _0 ,$

$\overrightarrow r = \int {\left( { - g\,t\overrightarrow k + \overrightarrow v _0 } \right)\operatorname{d} t = - \frac{g} {2}t^2 \overrightarrow k + \overrightarrow v _0 \,t} + \overrightarrow r _{0\,.}$

Mientras el vector velocidad siempre tiene direccion tangencial, puede estar dirigido opcionalmente el vector aceleracion. En un analisis profundo, la aceleracion se descompone en dos componentes, en la una direccion es tangencial (aceleracion tangencial) y la otra esta en direccion vertical (aceleracion normal).

La aceleracion tangencial cambia solo el valor de la velocidad (esta es la rapidez)

Para esta descomposicion de los vectores de la aceleracion introducimos la curva s, este es el largo de la trayectoria, que recorre la particula en la curva. Este arco cuenta con un punto cero escogido, que de todas formas aquí no juega ningún papel, aquí solo necesitamos el diferencial ds del arco. Además introducimos el vector unitario tangencial t y hacemos uso de la geometria diferencial. El vector unitario tangente t es el vector

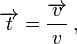
$\overrightarrow t = \frac{{\overrightarrow v }} {v}\,,$

así denominado, es igual al vector v dividido para su modulo v. Este modulo es igual a la rapidez y es otra vez el desplazamiento sobre la curva sobre el tiempo. Asi es:

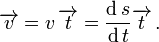
$\overrightarrow v = v\,\overrightarrow t = \frac{{\operatorname{d} s}} {{\operatorname{d} t}}\overrightarrow t \,.$

Si diferenciamos para el tiempo tenemos que

$\overrightarrow a = \frac{{\operatorname{d} ^2 s}} {{\operatorname{d} t^2 }}\overrightarrow t + \frac{{\operatorname{d} s}} {{\operatorname{d} t}}\frac{{\operatorname{d} \overrightarrow t }} {{\operatorname{d} t}} = \frac{{\operatorname{d} ^2 s}} {{\operatorname{d} t^2 }}\overrightarrow t + \frac{{\operatorname{d} s}} {{\operatorname{d} t}}\frac{{\operatorname{d} \overrightarrow t }} {{\operatorname{d} s}}\frac{{\operatorname{d} s}} {{\operatorname{d} t}} = \frac{{\operatorname{d} ^2 s}} {{\operatorname{d} t^2 }}\overrightarrow t + v^2 \frac{{\operatorname{d} \overrightarrow t }} {{\operatorname{d} s}}\,.$

Aqui la longitud del vector unitario tangencial t es constante (cercano a 1), esta el vector desplazamiento dt/ds - cuando no es igual a cero - verticalmente hacia t.

De la geometria diferencial tenemos, que el vector desplazamiento dt/ds

tiene la direccion del vector unitario normal n y
el valor k = 1/ρ

De aquí es k la curvatura de la curva en el punto observado y ρ su radio de curvatura. El vector unitario normal n es dirigido hacia (momentaneamente) a un punto medio de la curvatura (hacia dentro).

Siguiendo esto

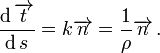
$\frac{{\operatorname{d} \overrightarrow t }} {{\operatorname{d} s}} = k\overrightarrow n = \frac{1} {\rho }\overrightarrow n \,.$

Con esto nos da como resultado

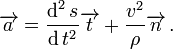
$\overrightarrow a = \frac{{\operatorname{d} ^2 s}} {{\operatorname{d} t^2 }}\overrightarrow t + \frac{{v^2 }} {\rho }\overrightarrow n \,.$

El vector a esta entre t y n' dirigido, en el plano de la curva en un determinado punto.

El modulo de la aceleracion tangencial es - como se esperaba:

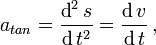
$a_{tan} = \frac{{\operatorname{d} ^2 s}} {{\operatorname{d} t^2 }} = \frac{{\operatorname{d} v}} {{\operatorname{d} t}}\,,$

el modulo de la aceleracion normal es

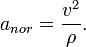
$a_{nor} = \frac{{v^2 }} {\rho }.$

Este par de ecuaciones tienen su interpretacion: La aceleracion de una particula da lugar a la aparicion de una fuerza. La direccion de esa fuerza determina la direccion de la aceleracion. La componente tangencial de la aceleracion causa un cambio en la velocidad, la componente normal de la aceleracion causa la curvatura de la curva. El radio de curvatura de la curva en un determinado punto resulta de la aceleracion normal y de la velocidad así:

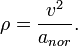
$\rho = \frac{{v^2 }} {{a_{nor} }}.$

CINEMATICA

ACELERACION

Aceleración

No hay comentarios:

Publicar un comentario